Tel. 01 / 526 48 46
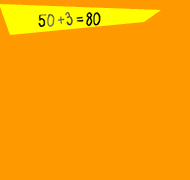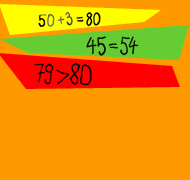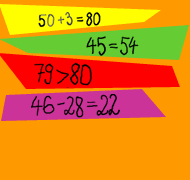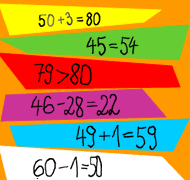
Viele Fehler – ein Prinzip: Die Schwierigkeiten rechenschwacher Kinder mit zweistelligen Zahlen folgen einer „inneren Logik“ – und können deshalb auch bewältigt werden!
In Nummer 1 des „Österreichischen Rechenschwäche Magazins“ (pdf, 277KB) wurde dargestellt, welche Materialien sinnvoll in der Erarbeitung des Zahlenraumes 10 mit rechenschwachen Kindern eingesetzt werden können.
Der vorliegende Artikel schließt daran an. Wesentlich zu seinem richtigen Verständnis sind aber die bereits im Vorgänger-Artikel erläuterten „Grundsätze“ für die Arbeit mit rechenschwachen Kindern im Allgemeinen und für den Einsatz von Material im Besonderen. Die wesentlichen dieser Grundsätze seien zur Vermeidung von Leerläufen oder gar Fehlern hier noch einmal kurz zusammengefasst:
Die Ausführungen in diesem Magazin können dafür wertvolle Anregungen geben. Wer aber bei der Umsetzung in eine Überforderungssituation gerät, sollte im Interesse des Kindes nicht zögern, frühzeitig professionellen Rat einzuholen.
Jede in sich noch so stimmige Fördermaßnahme kann wirkungslos verpuffen, ja sogar kontraproduktiv wirken, wenn sie zum falschen Zeitpunkt erfolgt, d.h.: wenn das Kind noch nicht über die Voraussetzungen für das Verständnis dieser Maßnahme verfügt.
Das ist bei Kindern mit Rechenstörungen in der Regel nur dann zu erreichen, wenn das Kind in einer ersten Phase selbst mit dem Material hantieren kann. Das „Anschauen“ ist also nicht der Witz beim Einsatz von sogenanntem Anschauungs-Material“.
Hier bedarf es – je nach Aufgabenstellung – verschiedenster vermittelnder Eingriffe durch die Betreuungsperson. Das Prinzip dabei sollte sein, dem Kind gerade so viel Materialhilfe zu gewähren, dass Frustrationen vermieden werden – aber auch so wenig, dass die geistigen Möglichkeiten des Kindes im Sich-Vorstellen und Abstrahieren voll ausgereizt werden.
Wird Zahl nur als Position (und nicht als Gesamtheit von soundsovielen Einern) gedacht, dann unterscheidet sich die „zehnte Position“ nicht wesentlich von der „neunten“ oder „elften“: Der Zehner kann nicht als „Bündelung“ von 10 Einern begriffen werden.
Im Sinne der oben formulierten Grundsätze“ ist es notwendig, sich zunächst das typische „Fehlerbild“ einer Rechenstörung in Bezug auf zweistellige Zahlen klarzumachen. Erst dann wird verständlich, welche Gegenmaßnahmen in diesem Bereich zielführend sein können.
Das Denken über zweistellige Zahlen ist bei den meisten Kindern mit Rechenstörungen einfach nur die Fortsetzung ihres – fehlerhaften – Denkens über einstellige Zahlen: Bei Zahlen wird nicht ein „Mehr“ oder „Weniger“ gedacht.
Es wird also nicht die Gesamtheit einer Anzahl von Einern damit verbunden. Sondern das Kind denkt Zahl (vorwiegend) als „Position“, als „Rangplatz“: Bei „9“ denkt das Kind nicht mit, dass hier 9 Einer in ihrer Gesamtheit vorliegen, die man deshalb auch beliebig in 5 + 4 oder 6 + 3 … Einer gruppieren könnte.
Sondern bei „9“ denkt das Kind an die „9. Station” in der Zahlenreihe. Und die „9. Station“ steht mit all den anderen „Stationen“ nur in einer Beziehung: Dass diese entweder „vorher“ oder „nachher“ kommen.
Aus dieser Denkweise ergibt sich einerseits die Notwendigkeit, zu zählen: Zahlverknüpfungen können nur dadurch gelöst werden, dass in der Zahlenreihe einzeln „hinauf- oder hinuntergehüpft“ wird.
Das geschieht zumeist mithilfe der Finger, auch noch in der dritten, vierten Volksschulklasse, sogar bis in die Sekundarstufe hinein. Eine Alternative dazu stellt nur das Auswendigmerken dar. Da aber jede Mengen-Vorstellung der Zahl fehlt, fehlt dem Gedächtnis auch die entscheidende Merkhilfe für das Speichern der Mengen-Beziehungen.
Darum klappt das Auswendigmerken der Grundaufgaben zumeist nur mit erheblicher Verzögerung – wenn überhaupt. Anregungen, wie gegen diese Schwierigkeiten vorgegangen werden kann, wurden in Nummer 1 des Österreichischen Rechenschwäche Magazins gegeben.
Aus der charakterisierten Denkweise über die Zahlen bis 9 ergibt sich aber andererseits auch, dass das Kind die Zahl 10 kaum als das verstehen kann, was sie ist: Die erste „Bündelung“ von genau
10 Einern zu einer neuen „Stelleneinheit“, genannt „Zehner“. Der Grundgedanke unseres Zahlensystems ist ja: Es gibt genau 10 Zeichen, von 0 bis 9, um anwachsende Anzahlen zu notieren. Also braucht es zusätzlich ein System von Stellen anwachsenden Wertes: An einer Stelle können höchstens 9 festgehalten werden. Kommt noch 1 dazu, werden diese 10 von der einen Stelle zu 1 von der nächst-höheren Stelle „gebündelt“. Dieser Grundgedanke setzt das Denken von Zahlen als Anzahl, Menge voraus. Wird dagegen immer nur an die Zahlen-Reihe gedacht, an das Vorher und Nachher, dann unterscheidet sich „10“ nicht grundsätzlich von „9“ oder „11“: So gedacht, ist 10 eben auch nur eine von vielen Positionen. Eine Position, von der ausgehend ich vor- oder zurückzählen kann, über die ich „drüberzählen“ kann. Was ein „Zehner“ ist, wie sich dieser „Zehner“ größenmäßig zu einem „Einer“ verhält (und später zu „Hundertern“, „Tausendern“, aber auch „Zehnteln“ …): All das wird dabei in keinster Weise mitgedacht.
So erklären sich die vielfältigen Schwierigkeiten rechenschwacher Kinder mit zweistelligen Zahlen. Hier seien nur die häufigsten in aller Kürze angeführt. Sie stellen teils verschiedene Stadien einer (leider fehlerhaften) Entwicklung dar, teils zeigt ein Kind mehrere dieser Probleme in Kombination, teils nur einzelne davon:
Wie oben dargestellt, sind die Probleme im Umgang mit zweistelligen Zahlen zumeist eine direkte Folge der Probleme im Umgang mit einstelligen Zahlen, also eine Folge der falschen Zahlauffassung eines Kindes. Sie können daher auch nur überwunden werden, wenn zuvor und – im Sinne der Automatisation – begleitend dazu an der Zahlauffassung des Kindes gearbeitet wird. Für die Aufarbeitung der Defizite im zweistelligen Bereich ergibt sich dann wieder eine Unterscheidung in gut geeignete und wenig geeignete Materialien.
sind alle Varianten von Einer-Würfeln/Plättchen mit maßstabgerechten Zehner-Stangen/Streifen (Dienes, Montessori, Legemax …): 10 hintereinander gelegte oder ineinander gesteckte Einer sind genauso lang wie 1 Zehner. Auch bei diesem Material kommt es freilich wieder entscheidend auf die Art der Verwendung an.
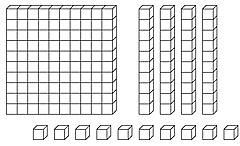
Geeignetes Material für die Erarbeitung des Zahlenraums 100 Die maßstabgerechte Darstellung 1 „Hunderter-Platte“ = 10 „Zehner-Stangen“ = 100 „Einer-Würfel“. Aber: „Legen“ alleine genügt nicht!
Als wenig wirksam erweist sich das auch noch so dauerhafte „Legen von Zahlen und Rechnungen mit Material“: Ein rechenschwaches Kind wird das in dieser Weise eingesetzte Material bestenfalls als Zählhilfe verwenden. Es kann dann die gestellte Aufgaben zwar mithilfe des Materials zählend bewältigen, bleibt aber ganz in seiner fehlerhaften Denkweise behaftet. Ein Verständnis dessen, was Zehner und Einer sind, kommt dadurch nicht zustande.
Das Verständnis, auf das es zunächst – noch unter Ausklammerung der Zehnerüberschreitung – ankäme, wäre ja: Zweistellige Zahlen sind aus unterschiedlichen Größen „zusammengebaut“. Ein Zehner ist etwas anderes, ist mehr als ein Einer. Und der Zehner muss an einer anderen Stelle aufgeschrieben werden. Bei der geschriebenen Zahl lässt nämlich einzig und alleine die Stelle erkennen, ob mit „1“ ein Zehner oder ein Einer gemeint ist.
Deshalb ist es beim Rechnen so wichtig, die Stellen zu beachten. Wenn man das tut, ist es aber auch wieder gar nicht so schwer: Mit Einern und Zehnern kann ich genauso rechnen, wie ich das mit einstelligen Zahlen gelernt habe. 1 Zehner und noch 1 Zehner sind zusammen 2 Zehner, genauso, wie 1 Einer und 1 Einer weiterhin 2 Einer sind. Ich muss nur darauf aufpassen, dass ich auch wirklich die Einer zu den Einern dazugebe und die Zehner zu den Zehnern (oder Einer von den Einern wegnehme und Zehner von den Zehnern).
Diese Einsicht kann mit Material erleichtert werden, ergibt sich aber aus dem „Nachlegen“ von Rechnungen nicht von selbst. Zumal dann nicht, wenn das stellengerechte Hinlegen des Materials – auf Anweisung oder als gemerkte, aber nicht verstandene Regel – jedes Nachdenken darüber erübrigt, was wo hingeschrieben werden muss. Umgekehrt ist es aber eine erste zielführende Übung, wenn das Kind eine mit Material auch einmal ungeordnet gelegte Zahl in Ziffernschreibweise notieren muss.
Auf dem Tisch liegen dann zum Beispiel (in Schreibrichtung) zuerst 4 Einer, dann 1 Zehner. Das Kind muss selbst überlegen, ob es 14 oder 41 dafür schreiben muss. Dann werden aber auch wieder zuerst 4 Zehner, rechts davon 3 Einer gelegt: Die Überlegung „Wo schreibe ich die Zehnerstangen hin, wo die Einerwürfel?“ soll dem Kind gerade nicht erspart bleiben, weil es ja genau auf die Einsicht in die Bedeutung der Stelle einer Ziffer ankommt.
In einer zweiten Phase kommt es dann aber gerade darauf an, diese Einsicht auch materialunabhängig abzusichern.
Ein Immer-wieder-Legenlassen birgt sogar die Gefahr in sich, dass das Nachdenken darüber, „welches Zeichen steht für die Zehner, welches für die Einer“ gerade nicht stattfindet: Das Nachdenken erübrigt sich ja durch den Augenschein. Es muss also nun der tatsächliche Material-Einsatz abgelöst werden durch ein konsequentes Sprechen über das Material, welches verwendet werden müsste.
Das Kind soll also angeben, wieviele Zehner-Stangen und Einer-Würfel für eine Zahl genommen werden müssten – ohne dass es dann noch nötig wäre, das Material tatsächlich auf den Tisch zu legen. Aufschreiben lässt sich dies, an einem Beispiel, in der Form
15 = 1 Z + 5 E
Umgekehrt soll das Kind eine in ihren „Stellen-Bestandteilen“ vorgegebene Zahl in Ziffernschreibweise aufschreiben. Also z.B.
1 Z + 7 E = 17
Im nächsten Schritt aber auch
5 E + 1 Z = 15
An Aufgaben wie
2 Z = 20 bzw. 2 E =2
lässt sich sodann die Bedeutung der Null im Stellenwertsystem klären.
Auf dieser Basis sind Aufgabenstellungen wie „10 + 3“ bzw. „5 + 10“ lösbar, wobei darauf geachtet werden muss, wie die Lösung erfolgt: Ein Kind, das hier zählen muss, hat eben das Wesentliche nicht verstanden und bedarf weiterer Überlegungen.
Fehler wie
3 E + 1 Z = 31 ?
sind durchaus „erwünscht“: als willkommene Gelegenheit, um Missverständnisse erstens zu entdecken und zweitens aufzuarbeiten.
für diesen ersten Zweck (Absicherung der getrennten Behandlung von Zehnern und Einern als unterschiedliche Größen, die an unterschiedlichen Stellen aufgeschrieben werden müssen) sind alle jene Materialien, in denen die Einheit des Zehners erst durch die aktive Wahrnehmungs- und Abstraktionsleistung des Kindes hergestellt werden muss.
Das gilt erstens für den Zahlenstrahl:
Der Zehner ist hier nur als Gesamtheit von 10 Einerstrecken „anschaulich“, also in Form der Gesamt-Strecke von der Markierung 0 bis zur Markierung 10. Diese Einheit kann ein Kind aber nur „sehen“, wenn es sie bereits weiß. Umgekehrt wird dieses Wissen durch noch so intensives „Anschauen“ des Zahlenstrahles nicht befördert:
Der „durchnummerierte Zahlenstrahl“ verführt geradezu zum rein zählenden Rechnen (hier am Beispiel „7 + 5“ dargestellt). Der „Zehner“ als Einheit von 10 Einern ist an ihm nur durch eine „aktive Interpretation“ als Längenmodell (Zehnerstrecke = 10 Einerstrecken) erkennbar. Diese Interpretation ist für ein Kind alles andere als selbstverständlich!
Was am Zahlenstrahl viel mehr „ins Auge springt“, ist folgendes:
Die Fortsetzung über 9 bzw. 10 hinaus ergibt keinerlei Besonderheit. Weiterhin gibt es für jede neue in der Zählreihe hinzukommende Zahl eine eigene Markierung; die Markierung für 10 unterscheidet sich in nichts von der Markierung für 9 oder auch 11. Die Zehner-Bündelung wird also gerade nicht sichtbar, die Bedeutung einer Zehner-Stelle daher ebenfalls nicht.
Eines freilich leistet der (mit allen Einer-Markierungen versehene) Zahlenstrahl: Er kann als Zählhilfe dafür verwendet werden, auch im erweiterten Zahlenraum durch „Vor- und Zurückhüpfen“ Plus- und Minusaufgaben zu lösen. Gerade diese Lösungsstrategie sollte aber verhindert werden.
Ähnliche Überlegungen sprechen gegen die Verwendung einer Zwanziger- oder auch Hunderter-Kette oder eines Rechenrahmens. Der Zehner ergibt sich hier nur dann, wenn genau 10 Kugeln zusammengeschoben und als Einheit betrachtet werden. Diese „Betrachtungsweise“ wird durch die Farbgebung (zumeist je 5 Kugeln in einer Farbe), beim Rechenrahmen zusätzlich durch die tatsächliche „Bündelung“ von 10 beweglichen Kugeln an einer Stange zwar nahegelegt.
Dennoch ist es wahrscheinlicher, dass ein entsprechend disponiertes Kind anstelle der Einheit von je 10 Kugeln doch immer nur die Einzelheit der jeweils für sich betrachteten Kugeln wahrnimmt und denkt. Wieder „verkommt“ das Material auf diese Weise zur reinen Zählhilfe. Eine Einsicht in die neue, größere Stelleneinheit wird dabei aber nicht aufgebaut.
Aus anderen Gründen problematisch ist die Verwendung von Geld als Rechenmaterial: Zum einen ist Geld in keinster Weise „anschaulich“. Dass ein Zehner „gleich viel“ ist wie 10 Einer, kann nicht „gesehen“ werden – das muss man schon wissen. Zweitens wird die Zehner-Einer-Ordnung des Geldes von nicht-dekadischen Ordnungsprinzipien überlagert (50-, 20- und 5-Euro-Scheine, 2-Euro-Stück), was eine zusätzliche Quelle von Verwirrung darstellen kann.
Der zentrale Gedanke des Stellenwertsystems und Schlüssel für alles weitere ist, wie ausgeführt, der „Bündelungsgedanke“” oder „Tauschgedanke“ des Inhalts:
10 Einer = 1 Zehner
Gute Chancen für eine nachhaltige Klärung dieses Gedankens bieten Aufgabenstellungen, in denen der „Austausch“ von
10 Einern und einem Zehner sich als notwendig zur Lösung erweist.
Das ist in Aufgaben wie
20 – 1 oder 20 –5
der Fall: Wenn von einer reinen Zehnerzahl Einer weggenommen werden, findet der „Tausch“ eines Zehners in 10 Einer statt. Dieser Tausch wird freilich nur dann zwingend, wenn die Aufgabe mit Stangen- und Würfelmaterial durchgeführt werden soll; bei einer zählenden Lösung der Aufgabe tritt der Tausch gerade nicht ins Bewusstsein des Kindes.
1. Ausgangspunkt ist eine Aufgabenstellung vom Typus „Z – E“, beispielsweise
70 –5
Das Kind wird aufgefordert, diese Aufgabe mit Stangen- und Würfelmaterial durchzuführen. Vorausgesetzt ist das Operationsverständnis: 7 Z sind zuerst vorhanden, dann muss ich davon 5 Einer wegnehmen. Die Kinder nehmen also 7 Zehnerstangen aus der Materialkiste – und sollen nun 5 Einer wegnehmen.
2. „Das geht ja gar nicht!“ – Diese Einsicht wäre der erste Schritt auf dem Weg zum Verstehen. Das Kind muss das Problem der Aufgabenstellung als solches erst einmal erleben und zur Kenntnis nehmen. Stattdessen sind hier natürlich Fehler der Art zu erwarten, dass ein Kind von den 7 Zehnerstangen 5 Zehnerstangen wegnimmt und die Aufgabe als gelöst betrachtet. Solche Fehler sind produktiv und sollten daher keineswegs vermieden werden. Wesentlich wäre nur, dass das Kind – durch entsprechende Kontrollfragen – den Fehler nachträglich selbst erkennt: „Sage mir noch einmal, wasdu weggeben sollst: 5 Einer, 5 Zehner oder 5 Würstl?“ – „5 Einer!“ – „Und, hast du das auch gemacht?“
3. Ist das Problem klar benannt, wird auch die Lösung für das Kind zumindest nachvollziehbar: Ich soll Einer wegnehmen, es sind aber keine Einer da. Ich habe aber Zehner – und Zehner kann man in Einer umtauschen. Also: Ich tausche einen von meinen Zehnern in 10 Einer um. Dann erst kann ich die gewünschten 5 Einer weggnehmen.
4. Erst wenn Tausch und Wegnehmen am Material vollständig durchgeführt wurden, wird nachträglich aufgeschrieben, was sich an Zehner- und Einerstelle als „Lösung“ ergeben hat: Ein Zehner wurde von den 7 getauscht, also sind es jetzt nur noch 6 Zehner. Von den 10 eingetauschten Einern wurden 5 weggenommen, es bleiben also noch 5 Einer. Insgesamt ergibt sich also
70 – 5 = 65
5. An einer oder mehreren weiteren Aufgaben desselben Typs wird zunächst darauf hingearbeitet, dass das Kind selbständig in der Lage ist, die Handlung mit Material durchzuführen und das Ergebnis dieser Handlung auch symbolisch festzuhalten.
6. Sollte das Kind dabei Schwierigkeiten zeigen, käme es darauf an, es mit „strukturierenden Fragen“ doch zum Nachvollzug zu befähigen – aber gerade nicht, ihm die Handlung immer wieder „vorzumachen“.
7. Auf einer nächsten Stufe sollte das Kind dazu ermutigt werden, zumindest Teile der Handlung in Gedanken vorwegzunehmen – also gerade nicht mit Material selbst durchzuführen. Dafür kann wieder das Material zwar zunächst auf den Tisch gelegt werden. Mit Blick auf das Material kündigt das Kind an, was es tun will. Dann aber wird das Material mit einem Tuch verdeckt. Die Handlung erfolgt nun entweder unter dem Tuch – oder, wenn möglich, überhaupt nur noch in der Vorstellung. Wiederum sollte im Falle von Schwierigkeiten versucht werden, durch gezielte, die Aufmerksamkeit des Kindes lenkende Fragen einen Nachvollzug – jetzt eben bereits in der Vorstellung – zu ermöglichen.
8. Nicht zielführend wäre es, die vollständige Materialhandlung immer wieder unverändert durchführen zu lassen und darauf zu setzen, dass alleine dadurch die Ablösung vom Material mit der Zeit quasi „von selbst“ erfolgen wird: Bei Kindern mit Defiziten im „Vorstellen“ und „Verinnerlichen“ ist es damit einfach nicht getan.
9. Auf einer „vorletzten“ Stufe vor Erreichen der rein symbolischen Ebene wird eine Aufgabe dieses Typs, z.B. 60 – 2, gänzlich ohne Material gelöst. Das Kind bekommt aber wenn nötig genaue Anweisungen, worauf es jeweils seine Aufmerksamkeit richten soll.
Ein „Musterdialog“ könnte etwa so ablaufen:
„Überlege, was du machen sollst!“
„Ich soll 2 Einer weggeben.“
„Wie viele Einer hast du?“
„Gar keinen.“
„Wie soll das dann gehen?“
„Ich muss einen Zehner tauschen!“
„Sehr gut. Dann überlege gleich: Wie viele Zehner wirst du dann noch haben?“
„Noch 5!“
„Spitze! Schreib’ das gleich im Ergebnis auf! …Was machst du als nächstes?“
„Weiß’ nicht!“
„Hm. Was hast du denn gerade gemacht?“
„Einen Zehner getauscht!“
„Und was hast du dafür bekommen?“
„Ach ja, 10 Einer! Jetzt nehme ich 2 Einer weg. Dann sind es noch 8 Einer. Die schreib’ ich an die Einerstelle, macht als Ergebnis: 58!“
„Super! Spitzenklasse!“
Ist das Kind erst einmal so weit gekommen, dann ist der weitere Weg zur Automatisation tatsächlich nur noch eine Frage von Wiederholung und Übung. Der Tauschgedanke ist damit freilich erst in einer Anwendung erarbeitet, als „Entbündelung“ von einem Zehner zu zehn Einern. Die Übertragung auf andere Problemstellungen erfordert weitere Erarbeitungsschritte, je nach Kind auch weiteren Einsatz von Material.
Der Zahlenstrahl wurde oben als „wenig geeignetes Material“ besprochen. Dies verlangt eine Präzisierung. Wenig geeignet ist der Zahlenstrahl für das Ausgangs-Problem des Inhalts: Wie kann mit einem Kind ein Grundverständnis von Zehnern und Einern erarbeitet werden?
Ist dieses Grundverständnis, einschließlich des Tauschgedankens 1 Z = 10 E, aber einmal vorhanden, dann eignet sich der Zahlenstrahl vorzüglich für vielfältige Übungen zum Aufbau eines „Zahlenraumes“. Allerdings ist auch hier wieder entscheidend, wie der Zahlenstrahl verwendet wird. Und zuvor schon: in welcher Weise der Zahlenstrahl selbst dem Kind verständlich gemacht wird. Denn die Darstellung von Zahlen am Zahlenstrahl wirft in sich eine Vielzahl von Problemen auf – nicht nur, aber speziell für Kinder mit Rechenstörungen. Um nun den Zahlenstrahl als Mittel für den Aufbau einer Zahlenraumvorstellung nutzen zu können, ist es notwendig, ihn als „Längen-Modell“ der Zahlen zu begreifen: Die Zahl 10 am Zahlenstrahl ist weder das Stricherl, unter dem „10“ geschrieben steht, noch das geschriebene „10“ selbst. Sondern 10 am Zahlenstrahl ist die gesamte Strecke, die beim „Stricherl über der 0“ beginnt und beim „Stricherl über der 10“ endet. Diese „Zehnerstrecke“ ist genau 10 „Einer-Strecken“ lang. Und 100 ist die Strecke vom „0-Stricherl” bis zum „100-Stricherl” und als solche genau 100 Einerstrecken = 10 Zehnerstrecken lang.
Dieses Verständnis entspricht gerade nicht dem „natürlichen“ Zahlenstrahl-Verständnis eines rechenschwachen Kindes. Dieses wird den Zahlenstrahl erst einmal als reine Zählhilfe verwenden:
„Nach 9 kommt 10, dann 11, dann 12.“ Die Zahlen werden also wieder nur, und durch den Zahlenstrahl scheinbar bestätigt, als Positionen genommen. Damit fehlt aber auch jede Grundlage für den Aufbau eines strukturierten „Zahlenraumes“.
Der Zahlenstrahl als „Längen-Modell“ macht aus dem Größenvergleich zweier Zahlen einen Vergleich von Strecken unterchiedlicher Länge: „28“ sind 2 Zehnertstrecken, 8 Einerstrecken, „82“ dagegen 8 Zehnerstrecken, 2 Einerstrecken.
1. Erarbeitung des Verständnisses für Längen-Messung als solche: Um den Zahlenstrahl zu verstehen, müssen die Kinder folgendes durchschaut haben: Das Messen von Längen besteht darin, festzustellen, wie oft eine vorgegebene Länge („Einheit“) in der zu messenden Länge „Platz hat“. Die Kinder haben zu diesem Zeitpunkt das Messen oft als bloßes „Ablesen einer Ziffernfolge von einem Maßband“ begriffen. Der Gedanke an eine „Einheit“ fehlt dabei völlig. Ein solches Vor-“Verständnis“ von Messen reicht für das Verstehen des Zahlenstrahls nicht aus.
2. Erarbeitung des Zahlenstrahls als Mess-Anordnung in diesem Sinne: Die vorgegebene Einheit „1“ oder „Einerstrecke“ wird immer wieder hintereinandergelegt. Die Markierungen werden dabei sinnvollerweise zunächst nicht nummeriert: „5“ zum Beispiel soll am Zahlenstrahl als
1 + 1 + 1 + 1 + 1
verstanden werden, also als die Gesamtstrecke, die sich durch 5 hintereinandergelegte Einerstrecken ergibt.
3. Erst wenn dieses Verständnis abgesichert ist, empfiehlt es sich, die Markierungen zu nummerieren. Weiterhin muss aber bei der Verwendung des Zahlenstrahls darauf geachtet werden, dass 5 nicht als „Stricherl über der (Ziffer) 5“ verstanden wird, sondern als Gesamtstrecke von 0 bis zu der mit 5 bezeichneten Markierung.
4. Bei Kindern mit Rechts-Links-Problemen kann es – einer Anregung von Jens Holger Lorenz folgend – helfen, den Zahlenstrahl nicht horizontal, sondern vertikal anzuordnen: Die hinzukommenden Einer-Strecken werden dann also „nach oben hin“ angefügt.
5. Der Zahlenstrahl bis 100 wird in gleicher Weise erarbeitet: „100“ ist nicht als die „Endmarkierung“ dieses Zahlenstrahles zu verstehen, sondern als Gesamtstrecke von 0 bis dorthin.
6. Zur Absicherung dieses Verständnisses empfiehlt es sich, Größenvergleiche zweistelliger Zahlen am Zahlenstrahl durchführen zu lassen: Was ist mehr, 87 oder 78? Dafür wird die Gesamtstrecke aus 8 Z-Strecken und 7 E-Strecken in einer Farbe, die Gesamtstrecke aus 7 Z-Strecken und 8 E-Strecken in einer anderen Farbe am Zahlenstrahl nachgezeichnet. Dem „Mehr“ der einen Zahl entspricht am Zahlenstrahl so ein „Länger“ der entsprechenden Strecke.
7. Erst auf Grundlage dieses Verständnisses wird nun auch ein Zahlenstrahl ohne Einer-Markierungen für das Kind handhabbar. Und nur an einem solchen Zahlenstrahl kann sichergestellt werden, dass die Orientierung im Zahlenraum im Bewusstsein der unterschiedlichen Quantität von Einern, Zehnern und Hundertern erfolgt – und nicht bloß zählend.
8. In weiterer Folge sollte dann auch in der Regel nur der nicht (vollständig) durchnummerierte Zahlenstrahl verwendet werden: Im Zahlenraum 100 also ein Zahlenstrahl nur mit Zehner-Markierungen, im Zahlenraum 1000 später sowohl Zahlenstrahle nur mit Hunderter- wie solche mit Hunderter- und Zehnermarkierungen, je nach Einsatz-Zweck.
1
Überprüfen Sie vor dem Einstieg in den zweistelligen Bereich, wie das Kind die Zahlen bis 9 versteht.
Wer 9 nur als „neunte Position“ auffasst, kann die Bündelung „10 Einer = 1 Zehner“ nicht begreifen.
2
Vor jedem Rechnen im zweistelligen Bereich müsste das Kind von sich aus die Stellen als unterschiedliche Größen begreifen. Das „Legen“ von Rechnungen mit Zehnerstangen und Einerwürfeln ist dafür bei vielen Kindern nicht ausreichend.
3
Das Bündeln und Entbündeln (10 E = 1 Z und umgekehrt) muss in einer ersten Phase vom Kind selbst an geeigneten Aufgabenstellungen handelnd erlebt werden. Der Übergang zum materialfreien Bündelnd und Entbündeln erfolgt bei vielen Kindern nicht einfach „von selbst“. Hier sind Zwischenschritte nötig.
4
Material, das eine rein zählende Lösung von Aufgaben im zweistelligen Bereich erlaubt oder gar nahelegt, sollte vermieden werden.