- Michael Gaidoschik
- Apr 20, 2013
- Empfehlungen, Mathematikunterricht, Zahlenraum, Zehnerübergang
Viele Wege führen über den Zehner
Einige Anregungen zur Behandlung von Aufgaben mit Zehnerübergang im ersten Schuljahr
Michael Gaidoschik, 2012
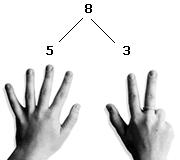Additionen und Subtraktionen mit Zehnerübergang (z.B. 7+8, 15-7) werden in Österreich üblicher Weise im zweiten Halbjahr des ersten Schuljahres erarbeitet. In vielen heimischen Schulbüchern wird als Rechenstrategie für solche Aufgaben das sogenannte „Teilschrittverfahren“ mit „Zehnerstopp“ alternativlos vorgeschrieben („Rechne so!“).
Für die Lösung beispielsweise der Aufgabe 7 + 8 wird also in vielen Büchern als einziger Lösungsweg der folgende vorgegeben:
1. Schritt: 7 + 3 = 10 (dabei mitgedacht: 8 = 3 + 5)
2. Schritt: 10 + 5 = 15
Andere, mathematisch gleichfalls richtige Strategien zur Lösung dieser und ähnlicher Aufgaben kommen in den meisten derzeit verwendeten Schulbüchern entweder gar nicht vor oder werden erst zu einem sehr viel späteren Zeitpunkt nachgereicht. Von dieser Art, Aufgaben mit Zehnerüber- und –unterschreitung im Unterricht zu behandeln, wird im folgenden Beitrag ganz entschieden abgeraten.
Das wegweisende Forschungs- und Entwicklungs-Projekt „mathe 2000“ feiert heuer sein 25-Jahr-Jubiläeum. Rechtzeitig zum Fest-Symposion am 22. September 2012 an der TU Dortmund ist der Sammelband „Zahlen, Muster, und Strukturen. Spielräume für aktives Lernen und Üben“ erschienen, den wir hiermit allen, die an einem zeitgemäßen Mathematikunterricht Interesse haben, wärmstens empfehlen.
KIRA (Kinder rechnen anders) und PIK AS (Prozess- und inhaltsbezogene Kompetenzen – Anregungen zur fachbezogenen Schulentwicklung) sind zwei Projekte an der TU Dortmund (Institut für Entwicklung und Erforschung des Mathematikunterrichts), die sich die Weiterentwicklung des Mathematikunterrichts zum Ziel gesetzt haben. Auf den Webseiten der beiden Projekte finden Lehrkräfte eine Fülle von Anregungen für einen Mathematikunterricht, der ALLEN Kindern zugute kommt: den „rechenschwachen“ ebenso wie den „rechenstarken“.
Die Bildungsstandards M4, an denen künftig der Mathematikunterricht in Österreichs Volksschulen gemessen werden soll, enthalten richtige, wichtige Ziele – Ziele des Mathematikunterrichts in der Grundschule, die von der aktuellen Mathematik-Fachdidaktik seit vielen Jahren formuliert und begründet werden. Aber wie erreicht man, dass diese Ziele auch tatsächlich von möglichst vielen Kindern erreicht werden?